
本文针对卧式四轴机床上加工大型弧面的一种新的方法进行了系统分析,建立了数学模型,编写了全参数化宏程序,提高了弧面的加工效率,保证了产品的加工品质。
1.加工分析
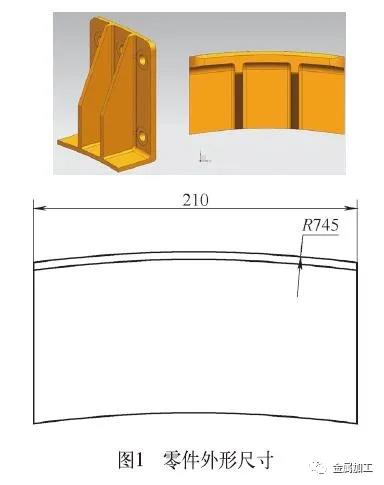
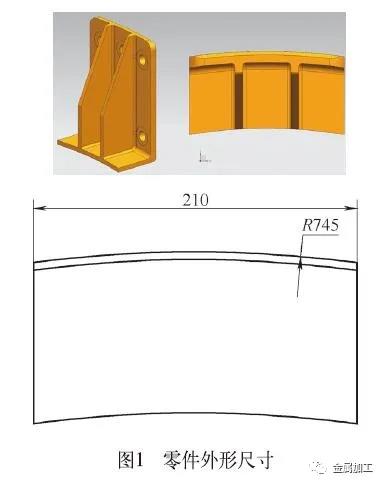
弧面是一种常见的加工特征,加工方法也多种多样。大型弧面的加工在日常的机械加工中还是一个难点。如图1所示零件,其外形尺寸为280mm×210mm×114mm,外侧弧面半径为745mm。该弧面粗加工可以采用传统的加工方法,精加工时,初步选用沿圆周方向进行铣削,但由于弧面长度为280mm,若两边接刀加工,则刀具悬伸较长,加工过程容易出现颤动,刀具磨损加剧,寿命低,加工质量差、效率低;另外,也可以沿圆弧步进,两边接刀,利用刀具的侧刃,沿母线进行加工,加工刀具选用球形刀具或者R角铣刀。由于弧面半径大,为保证表面粗糙度要求,则需选用较小的步距进行逼近加工,加工效率特别低,其加工时间约两个工时。
经过优化选择,选用面铣刀沿母线进行加工。装夹找正时,使圆弧中心轴线与工作台面保持垂直。工作台每旋转一次,刀具沿母线进行一次切削,依次往复加工,直至弧面成形。该方法难点在于宏程序的编制。
2. 技术方案
弧面的中心若与四轴机床的工作台中心重合,则编程会很简单。通常情况下,由于受空间限制,弧面经常会不与工作台的中心重合,这为编程带来很大难度。为保证加工方法的通用性,以下主要针对上述加工方法一般情况进行讨论分析。其他加工方法应用已比较普遍,不再赘述。
(1)数学模型分析 图2中三张图片分别为工件装夹初始位置、加工初始位置和加工终点位置三种状态下的示意图,其中O点为工作台的中心位置,A点为加工的起始位置,B点为终止位置,C点为圆弧的初始位置。
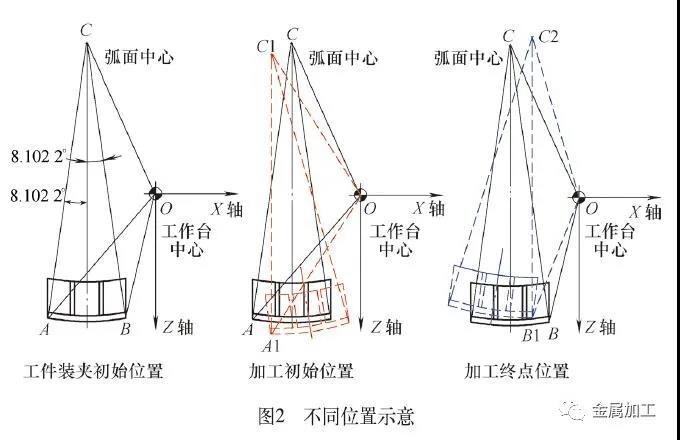
如图2所示,把X、Z轴零点设置在工作台中心位置,Y向零点设置在弧面的顶端。计算加工位置,然后沿Y向切削一次,依此往复,直至加工到终点位置。
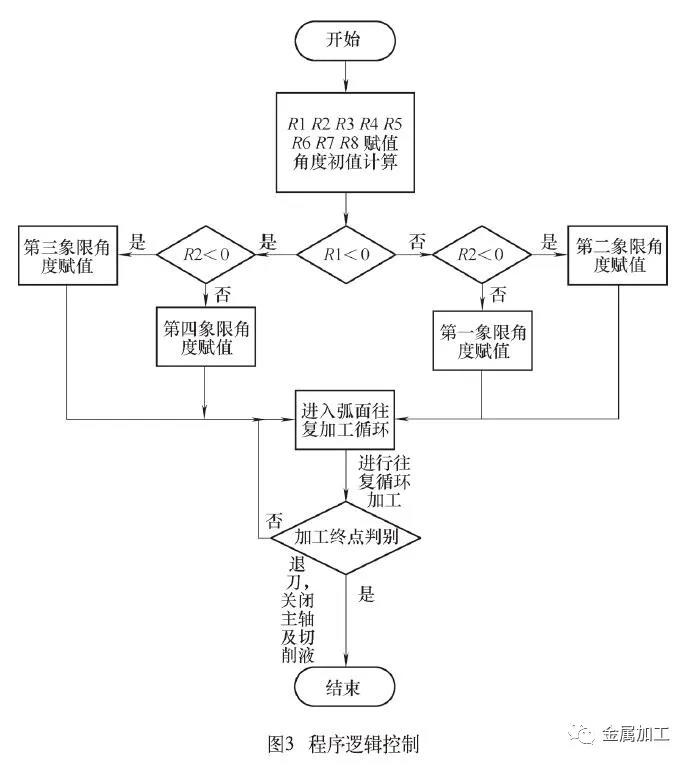
(2)宏程序编制 程序逻辑控制图如图3所示。先对各参数赋值,然后依据弧面中心的坐标数值,对其所在的象限进行自动判别。对象限判别的目的是为了计算圆弧中心和工作台中心(零点位置)连线与Z轴正向之间的夹角。最后,进入加工阶段,开始按宏程序进行往复加工。
宏程序采用西门子系统指令进行编制计算,零点在工作台中心,Y向零点在工件的上表面,工作台每转0.5°,沿母线进给一次,需步进36次。经过计算,加工残余高度为0.007 1mm,满足技术要求。程序如下:
G54;设定坐标系
G64;启动连续切削模式
SOFT;圆滑增减速打开
FFWON;前馈控制打开
T1D1;调用φ50端面铣刀,选择1号刀具,调用1号长度补偿;用Vericut仿真时更改为T1M6
G0 X300Y60;初始定位Z500;快速运动到安全位置S1300M03;
R1=100;初始装夹位置R745圆弧中心X坐标
R2=-515;初始装夹位置 R745圆弧中心Z坐标
R3=-9;加工初始状态角度初值
R4=745;工件圆弧半径
R5=280;弧面长度
R6=25;刀具半径
R7=-1;方向控制变量,初始向下,设置为-1
R8=R7;圆弧中心位置判断及初始角度计算
R11=SQRT(R1*R1+R2*R2);圆弧中心相对工作台中心旋转半径
R 9 = A S I N ( R 1 / S Q R T ( R 1 * R 1 + R2*R2));
IF R1<0 GOTOF BB1;满足条件跳转,否则进行一、二象限角度判别
IF R2<0 GOTOF AA1;
R10=R9;第一象限角度判别计算
GOTOF BB;完成后跳出判别区域 AA1:
R10=180-R9;第二象限,角度判别计算
GOTOF BB;完成后跳出判别区域BB1:
IF R2<0 GOTOF AA2;第三、四象限初始角度判别
R10=R9
GOTOF BB
AA2:
R10=-180-R9;判别结束
BB:
G1 B=R3;
R16=R11*SIN(R10-R3);圆弧中心X坐标值
R17= R11*COS(R10-R3);圆弧中心Z坐标值
TRANS X=R16 Z=R17+R4;坐标偏移
G01Z0F2000;Z轴定位
G01X0F1500;X轴定位
G01Y=0-8*R6*1.2+(R8+R7)*(R5+ R6*2.4)/2;数字1.2为单边延伸系数。2.4为两边总延伸系数。
R7=-R7
R3=R3+0.5;度数递增
IF R3<=9 GOTOB BB;满足条件跳转
TRANS;坐标偏移取消
G0Z=IC(200);Z向退刀
X300Y300;移动到安全位置
G1C0F3000;工作台旋转至初始位置
M05;主轴停止
M09;冷却液关闭
M30;程序结束,系统复位
程序相关说明:
①在ZOX平面内进行角度计算,Z为横轴,X为纵轴。②注意工作台旋转时,顺时针为正,而坐标系逆时针旋转 为 正 。③ 圆 弧 初 始 位 置 坐 标值,通过对刀确定。④工作台的中心坐标,建议使用基准块进行校准,这样有利于减少零件的加工误差。
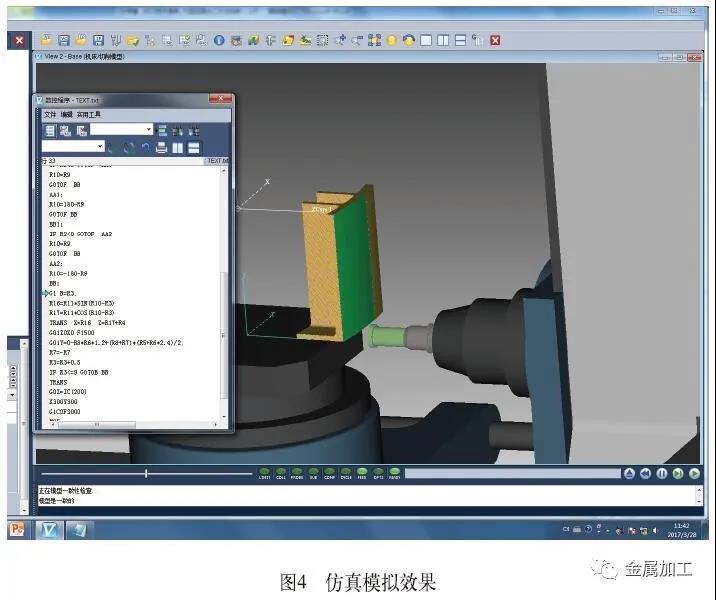
在仿真软件Vericut中对宏程序进行了仿真模拟,效果如图4所示。
3. 结语
本文提出一种比较高效的大型弧面加工方法,建立了加工数学模型,编写了通用的全参数化往复加工宏程序,针对不同的弧面,具有很好的适应性。经实际加工验证,相比传统的加工方法,弧面精加工效率提高了8倍左右。另外,加工过程更加平稳,加工品质得到很大程度提升。